- die Spezifität: Sie beschreibt die Fähigkeit des Analysenverfahrens, nur den gesuchten Analyten zu erfassen, wobei andere in der Probe anwesende Bestandteile/Merkmale das Analysenergebnis nicht beeinflussen,

- die Empfindlichkeit des Analysenverfahrens: Sie gibt die angezeigte Meßwertänderung pro Konzentrationsänderung an,

- die Genauigkeit im Sinne der Richtigkeit (keine systematischen Fehler) und der Präzision (Maß an Übereinstimmung zwischen Ergebnissen, wie sie bei wiederholter Anwendung eines festgelegten Analysenverfahrens auf dieselbe Probe gewonnen werden). Unpräzise Ergebnisse werden durch zufällige Fehler verursacht.

In der Regel werden Parallelbestimmungen angesetzt. Die so erhaltenenen Resultate sollen möglichst identisch sein und dem tatsächlichen Gehalt der Probe entsprechen. Es sind also zwei Gesichtspunkte, nach denen der Analytiker zunächst seine Ergebnisse beurteilt [103]:

- die Reproduzierbarkeit der ermittelten Resultate

- die Übereinstimmung mit dem Gehalt der Probe

Die Reproduzierbarkeit wird vom Zufallsfehler des Analysenverfahrens bestimmt. Je größer der Zufallsfehler ist, desto stärker weichen die Meßwerte bei der Wiederholung der Analyse voneinander ab und desto geringer ist die Präzision der Analyse. Je geringer die Präzision ist, desto unsicherer wird das Analysenergebnis sein. Zusätzlich können systematische Fehler auftreten, die das Ergebnis der Analyse verfälschen.

Ursachen für Zufallsfehler und systematische Fehler sind häufig [17] :

- die Inhomogenität von Proben,

- zufällige Fehler (z.B. Löslichkeitsbeeinflussungen durch Neutralsalz-konzentrationen) und systematische Fehler (z.B. Mitfällungserscheinungen) wenn die Proben chemischen Reaktionen unterworfen werden,

- Fehlerhaft justierte Meßgeräte.

Einige auftretende Fehler lassen sich auf die jeweiligen Eigenschaften des benutzten Analysenverfahrens zurückführen. Der Analytiker muß versuchen, die Zufallsfehler zu minimieren, und die systematischen Fehler auszuschalten. Systematische Fehler können mit Hilfe der analytischen Qualitätssicherung durch mehrere verschiedene Richtigkeits-Kontrollproben überprüft werden. Es sollten Proben verwendet werden, deren Gehalte über den gesamten Meßbereich des Gerätes verteilt sind. Liegen die Meßwerte dieser Proben überwiegend höher oder niedriger, so wird ein systematischer Fehler vorliegen.

Aufgabe des Analytikers ist demnach, die Qualität jedes von ihm angewandten Analysenverfahrens zu ermitteln, ggf. zu verbessern sowie sicherzustellen und zu dokumentieren, daß die erreichte Qualität zu jedem Zeitpunkt der Routineanalytik auch eingehalten wird. Erst dann kann von einem zuverlässigen Analysenverfahren gesprochen werden.

Die Qualitätssicherungsmaßnahmen spiegeln sich in dem 4-Phasen-Modell der analytischen Qualitätssicherung mit Hilfe statistischer Methoden [104], wie es im folgenden beschrieben wird, wider:

- In Phase I wird ein neues, insbesondere kalibrierbedürftiges Analysenverfahren auf seine Qualitätsmerkmale hin untersucht und ggf. verbessert und beschrieben.

- In Phase II, der sogenannten vorbereitenden Qualitätskontrolle, wird ein Analysenverfahren, dessen Qualitätsmerkmale bereits dokumentiert sind, für die Routineanalytik einsatzfähig gemacht. Hierzu zählen das Erreichen und die Wahrung einer ausreichenden Analysenqualität vor Beginn der Routineanalytik.

- Phase III umfaßt alle laborinternen Maßnahmen der Qualitätssicherung in der Routineanalytik, begleitet durch

- laborexterne analytische Qualitätssicherungsmaßnahmen der Phase IV (externe Qualitätssicherung in Form von Ringversuchen).

Während der Erstellung eines neuen Analysenverfahrens (Phase I) müssen also statistische Methoden angewandt werden, um Informationen über die aktuell erreichte Analysenqualität zu erhalten. Zudem müssen die Verfahrenskenndaten der linearen Kalibrierfunktion einschließlich der Präzisionsmaße bei jeder Kalibrierung des Analysenverfahrens, so z.B. nach Reagenzienwechsel und technischen Eingriffen in Analysengeräte, neu ermittelt werden.

Neben diesen Daten müssen schon bei Gewinnung der Analysenfunktion sogenannte Ausreißertests für die einzelnen Meßwerte durchgeführt werden. Der Test nimmt Meßwerte (z.B. eines Kalibrierexperiments) aus der Berechnung, die mit großer Gewißheit eine zufällige Abweichung vom Sollwert zeigen. Diejenigen Meßwerte, die als Ausreißer entdeckt werden, müssen bei der Ermittlung der Analysenfunktion herausgenommen werden. In [104] wird eindeutig gesagt:

Wird ... ein Ausreißer statistisch nachgewiesen, so muß als unabdingbare Forderung die Fehlerursache gesucht und eliminiert werden. Sodann ist die gesamte Kalibrierung zu wiederholen [104].

Bereits in Phase II, die mit dem „Einüben“ des Analyseverfahrens beginnt und mit der Vorbereitung einer Qualitätsregelkarte für die folgende Routine endet, müssen die Verfahrenskenndaten vorliegen. Es liegt daher nahe, bei jedem Analysenergebnis die grundlegenden statistischen Qualitätskenndaten der vorangegangenen Kalibrierung neu zu berechnen und in der Datenausgabe zu dokumentieren. Aufgrund der umfangreichen und zeitaufwendigen statistisch-mathematischen Operationen, die durchzuführen sind, drängt sich hier eine rechnergestützte Automation geradezu auf.

Folgende Kenndaten können für jede Analyse nach vorangegangener Kalibrierung automatisch ermittelt werden:

- Die Koeffizienten der Kalibrierfunktion:

- im Fall der linearen Kalibrierfunktion 1.Grades (y=a+bx): Achsabschnitt a und Steigung b als Maß für die Empfindlichkeit des Analysenverfahrens

- im Fall der Kalibrierfunktion 2.Grades (y=a+bx+cx²): Achsabschnitt a, Koeffizient b des linearen Gliedes sowie der Koeffizient c des quadratischen Gliedes; die aus der Funktion abgeleitete Empfindlichkeit E des Analysenverfahrens

- Verfahrensstandardabweichung als absolutes Präzisionsmaß der Kalibrierung

- Verfahrensvariationskoeffizient als relatives Präzisionsmaß

- Vertrauensbereich

Für die allgemeine Beurteilung des Analysenverfahrens kann darüberhinaus die Nachweis- und Erfassungsgrenze (Prüfgröße X_p) zur Validierung des unteren Arbeitsbereichsendes herangezogen werden.

Für die Bestimmung der Nachweisgrenzen können verschiedene Methoden benutzt werden:

- Die Leerwertmethode sieht die Berechnung der Nachweisgrenze aus der Unsicherheit des Blindwertes vor. Die Nachweisgrenze wird nach DIN 32645 für die Leerwertmethode aus der Standardabweichung der Leerwerte unter Berücksichtigung einer statistischen Sicherheit von 95% ermittelt. Die Schnellschätzung der Nachweisgrenze erfolgt nach dem 3s-Kriterium, wobei die 3-fache Standardabweichung der Leerwerte durch die Steigung der Kalibriergeraden (Empfindlichkeit) geteilt wird.

- Die Kalibriergeradenmethode ermittelt die Unsicherheit des Blindwertes durch Extrapolation der Regressionsdaten einer Kalibriergeraden. Hierfür können verschiedene statistische Sicherheiten zugrunde gelegt werden. Es werden in der Regel Vertrauensbereiche von 95% oder 99% gewählt.

Dem Prüfwert X_p liegt nach FUNK et al [104] der gleiche mathematische Algorithmus zugrunde, der in DIN 32645 (Nachweis-, Erfassungs- und Bestimmungsgrenze, Mai 1994) zur Schnellschätzung der Bestimmungsgrenze nach der Kalibriergeradenmethode verwendet wird. Im Unterschied zu der hier durchgeführten Berechnung (P=95%) werden in DIN 32645 die Integralgrenzen der t-Verteilung mit einer zweiseitigen Fragestellung und der Wahrscheinlichkeit P= 99 % angewandt. Zusätzlich wurde der Faktor K = 3 mit 1,2 multipliziert, während bei der Realisation des Auswerteprogramms noch der von FUNK et al eingesetzte Faktor K = 2 verwendet wurde. Auf einen Vergleich dieser mit unterschiedlichen Faktoren berechneten Erfassungs- und Bestimmungsgrenzen wird in Kapitel 10 näher eingegangen.

6.6 Statistische Verfahren der internen Qualitätssicherung

Im folgenden sei ein kurzer Überblick über die verwendeten statistischen Verfahren gegeben, die in das Auswerteprogramm implementiert wurden und auf die in den anschließenden Kapiteln Bezug genommen wird. Anhand der Beispiele, die mit dem fertiggestellten Programm in der Praxis gewonnen wurden, soll verdeutlicht werden, wie durch eine Automation dieser zahlreichen statistisch-mathematischen Operationen ein Hilfsmittel integriert wurde, durch welches der Analytiker bereits frühzeitig auf eventuelle Fehler hingewiesen werden kann.

6.6.1 Verfahrenskenndaten der linearen Kalibrierfunktion

Mittelwert:
Mittelwert:
Statistische Hilfsgrößen:	Qxx = åxi2 - 1/N × (åxi)2 Qyy = åyi2-1/N × (åyi)2 Qxy = å(xi ×yi) - (1/N × åxi × yi)
Steigung:	b = Qxy/Qxx
Achsabschnitt:	a =
Korrelationkoeffizient r: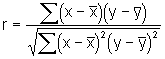
Reststandardabweichung:
Verfahrens-Standardabweichung:
Verfahrens-Variations-Koeffizient:
Prüfgröße Xp:

mit t(f =N-2, P = 95%, einseitig) und K = 2

6.6.2 Residuenanalyse zum Nachweis von Ausreißern bei der Kalibrierung

Es ergeben sich die Residuen d_i als vertikale Abstände der Meßwerte von der Regressionskurve.

Nach Eliminierung des Wertepaares mit dem größten Residuum als potentiellem Ausreißer aus dem Datenkollektiv wird eine neue Kalibriergerade mit der Anzahl der Konzentrationsstufen N_A2 und der Reststreuung s_yA2 berechnet. Die Prüfung erfolgt dann mit dem F-Test, bei dem die Reststreuungen s_yA1 und s_yA2 der beiden Geraden auf einen signifikanten Unterschied geprüft werden.

Der Prüfwert ergibt sich aus:

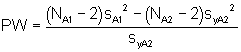
und wird mit dem Tabellenwert F (f₁ = 1, f₂ = N_A2 - 2, P = 95%) verglichen.

Ist der Prüfwert kleiner als der Tabellenwert, liegt kein Ausreißer vor, und die eliminierten Werte werden dem Datenkollektiv wieder zugefügt.

Abb.17 zeigt recht drastisch, wie stark Ausreißer-Meßwerte die Analysen­funktion beeinflussen. Ein Vergleich beider Analysenfunktionen und der statistischen Qualitätskenndaten verdeutlicht die Notwendigkeit der statistischen Prüfung.

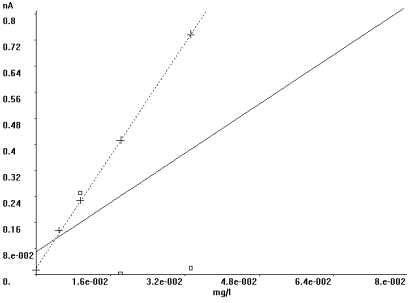Abb.17 Kalibrierfunktionen mit und ohne Ausreißer. + Meßwert, der im statistischen Sinne als korrekt anzusehen ist,  Meßwert, der als Ausreißer erkannt wurde.

6.6.3 Ergebnisangabe bei Verwendung der linearen Kalibrierfunktion

Analysenergebnis und Vertrauensbereich berechnen sich unter Verwendung der linearen Kalibrierfunktion zu :

                    Ergebnis ± VB ()

mit

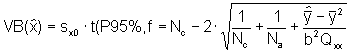
mit = Mittelwert aus N_a-Mehrfach-Meßwerten (N_a kann aber auch 1 sein)

                    Ergebnis =

6.6.4 Ergebnisangabe bei Verwendung von Mehrfach-Meßwerten; Grubbs-Ausreißertest

Zur Aufdeckung einzelner Ausreißerwerte von Mehrfach-Meßwerten einer Analyt- oder Probenkonzentration werden zunächst der Mittelwert und die Standardabweichung s der Analysendaten berechnet. Der Analysenwert x* mit der größten Differenz zum Mittelwert wird als potentieller Ausreißer zur Berechnung des Prüfwertes PW herangezogen:

Ist der Prüfwert PW > rM (f, P=95%), so liegt ein signifikanter Unterschied vor und der Wert x* wird markiert und eliminiert. Anschließend werden Mittelwert und Standardabweichung neu berechnet.

7 Realisierung der vollautomatischen analogen Voltammetrie

[104] Funk, W.; Dammann, V.; Donnevert, G.: Qualitätssicherung in der Analytischen Chemie, Verlag Chemie Weinheim (1992).